| Issue |
Sust. Build.
Volume 3, 2018
Zero Energy Mass Custom Homes
|
|
|---|---|---|
| Article Number | 3 | |
| Number of page(s) | 14 | |
| DOI | https://doi.org/10.1051/sbuild/2018002 | |
| Published online | 15 June 2018 | |
Research Article
Solar water heating systems for different buildings under a hot climate; parametric optimization and economic analysis
Architectural Engineering Department, College of Engineering, United Arab Emirates University,
P.O. Box 15551
Al Ain, UAE
* e-mail: kheira.anissa@uaeu.ac.ae
Received:
16
December
2017
Accepted:
14
May
2018
Building applied solar thermal systems are considered by different stakeholders an attractive alternative to traditional space and water heating systems. However, their performance depends largely on climatic conditions, water heating needs and operational parameters which, in turn, offer opportunities for performance optimization. The present research attempts to provide architects with a design decision tool that integrates solar thermal collectors efficiently to meet hot water demand for various building types inclusive of residential, commercial and industrial in a hot climate. The analysis is conducted numerically through a thermal model developed and executed in TRNSYS and validated experimentally. The parameters investigated include the collector tilt angle, azimuth angle and collector inlet fluid flow rate. Finally, the collector aperture area required per building foot print area is determined. The research revealed that for a 1000 m2 footprint building area of schools, offices, residential, factories and hospitals would require respectively 8 m2, 10 m2, 14 m2, 24 m2 and 38 m2 of the static collector installed at 24° tilt angle with optimal water flow rate. Additional operational aspects of collector tracking, and solar radiation concentration were investigated and further reduce the required collector area. A simple payback period analysis reveals a return on investment of 2 years applying subsidized tariff rates under the climatic conditions of, or similar to Dubai, in the United Arab Emirates.
Key words: solar water heating systems / building applied / parametric optimization / hot climate / performance assessment
© K.T. Aoul et al., published by EDP Sciences, 2018
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Dubai, in the United Arab Emirates (UAE) increased its energy demand from 33 742 to 43 093 GWh between 2010 and 2016, while adding 2639 MW electrical power capacity in the same period from 7361 to 10 000 MW (Fig. 1) indicating a sharp surge in its energy demand [1]. The capacity addition presented here is solely from gas, oil fired power plants, and does not include renewables. The curve shows that until 2015, the traditional power plants were merely meeting the demand. Afterwards, the demand surpassed the supply. In terms of energy consumption, the commercial sector leads with 47.5% followed by residential buildings at 28.5% as illustrated in Figure 2 as of 2016 [1]. This substantial energy needed in buildings contributes to carbon dioxide emissions, heightening the global warming effect [2] that can merely be addressed by integrating sustainable means of energy supply. Out of the total energy consumed in buildings, space and water heating needs range from 81% in cold climates [3] to 30% in hot climates [4] which justifies investing into alternative heating solutions to reduce the environmental footprint. The immense solar radiation potential reported in the UAE with measured average daily insolation of 4.98 kWh/m2 and peak intensity ranging between 900 and 1100 W/m2 in different seasons [5,6,7]. These statistics offer a promising source of heat supply through solar systems to meet hot water demand in UAE with the appropriate system sizing and configurations.
The performance of solar-assisted heating and cooling (SHC) systems was compared to the conventional cooling system for two building configurations in the UAE to determine optimal share of solar thermal in the building energy mix. The findings suggest a maximum solar penetration of 20% that results in an energy and CO2 savings of 176 kWh/year and 140 ton/year with a payback period of 4 years [8]. In another study, the solar thermal collector area and hot water tank volume were optimized for a solar powered absorption cycle under UAE's weather conditions. The findings reveal that a specific collector area of 6 m2/kWc and a specific tank volume of 0.1 m3/kWc offer an optimal design that reduced energy consumption by 47% and CO2 emissions by 12 tons/year compared to a conventional vapor-compression cooling system [9]. These limited experimental studies conducted in the UAE revealed that Solar Water Heating Systems (SWHS) are efficient and form an economically viable option to meet the hot water demand in buildings.
However, little is reported about optimal parameters that affect SHW performance inclusive of determining an optimal tilt angle (Φ) for the main UAE cities (Abu Dhabi and Dubai) [10,11]. This study considered the capital city, Abu Dhabi which lies at a latitude of φ = 24°. A detailed parametric optimization investigation is highly needed while considering various hot water demand patterns of different building typology. The current study attempts to numerically investigate collector parameters comprehensively to optimize the collector performance with regard to building types and hot water demands employing a TRNSYS thermal model [12]. The parameters considered include collector tilt angle, azimuth angle and collector inlet fluid flow rate. Additionally, the effect of inlet water temperature, collector tracking and solar radiation concentration were investigated. The objective of this study is to determine design parameters represented by the ratio of collector aperture area to building area for each of the studied building types while assessing its economic viability and system performance.
2 Methodology
The transient thermal model developed in TRNSYS is composed of a solar thermal collector and an auxiliary heating source. Simulations were carried out to assess the contribution and effectiveness of SWHS in meeting specific hot water demands in various building types. The building types considered include residential, schools, hospitals, offices and factories. For this investigation and comparison, all building types are considered to be 1000 m2 in size. Buildings with spatially different occupant loads, such as hospitals and schools, have been considered accordingly, with half of the building area dedicated to each. The occupant load, water demand and required water temperature are calculated from relevant codes [13,14]. Table 1 summarizes the input data parameters.
Hot water demand and water temperature per building type of a set area of 1000 m2.
2.1 Simulation model set up
The flat-plate solar collector is simulated using Hottel–Whillier steady-state model [16] which predicts the heat gain as a function of collector aperture area (Ac), number of identical collectors (nc) and weather conditions as presented in equation (1);
 (1)
(1)
The model employs overall energy gain efficiency factor (fr,k), total incident solar radiation (Iti), collective losses (Uc,k), temperature of fluid entering the collector (Ti) and ambient temperature (Ta) to calculate collector heat gain (Qc). The fr,k is an exponential function of the collector aperture area and thermal capacity (Cpc) as given in equation (2);
 (2)
(2)
The product of transmittance and absorptance of the collector absorber plate for beam radiation (τα)b, diffused-radiation (τα)d, and ground reflectance (τα)g are calculated by the trigonometric co-relation considering collector relative position to the incoming solar radiation given in equation (3);
 (3)
(Uc,k) is overall loss-coefficient by Klein composed of radiation and convection from top and bottom collector surfaces [16]. These losses are a function of number of glass covers (ng), collector fin efficiency (fc), number of collectors (nc), Stefan Boltzmann's constant (σ), emissivity of glass cover (ϵg), absorber plate emittance (ϵp) and loss coefficients for edges and bottom (Ube) as depicted in equation (4).
(3)
(Uc,k) is overall loss-coefficient by Klein composed of radiation and convection from top and bottom collector surfaces [16]. These losses are a function of number of glass covers (ng), collector fin efficiency (fc), number of collectors (nc), Stefan Boltzmann's constant (σ), emissivity of glass cover (ϵg), absorber plate emittance (ϵp) and loss coefficients for edges and bottom (Ube) as depicted in equation (4).
 (4)
(4)
The stratified thermal storage tank with variable inlets conditions is employed having an immersed coiled heat exchanger, with five segments for thermal lamination. The temperatures of hot water tank at the outer side (Thw2) and average temperature at inner side (Thwa) were calculated by using equations (5) and (6) [17].
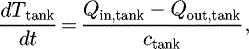 (5)
(5)
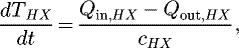 (6)
where Qin,tank and Qout,tank depend on heat exchanger temperature, ambient temperature and solar irradiation. The Qin,HX and Qout,HX depend on inlet fluid temperature and tank temperature. The temperatures Thw2 and Thwa are calculated by opting equations (7) and (8).
(6)
where Qin,tank and Qout,tank depend on heat exchanger temperature, ambient temperature and solar irradiation. The Qin,HX and Qout,HX depend on inlet fluid temperature and tank temperature. The temperatures Thw2 and Thwa are calculated by opting equations (7) and (8).
 (7)
(7)
 (8)where a and b are the coefficients of the differential equation in the form dT/dt = aT + b and bave = bTave.
(8)where a and b are the coefficients of the differential equation in the form dT/dt = aT + b and bave = bTave.
Figure 3 shows the information flow diagram for the micro-simulation of solar water heating and Figure 4 shows the flow diagram of TRNSYS for SWHS. The components of the SWHS considered are flat plate solar collector, water pump, storage tank and auxiliary electric heater. The system comprises of a 2 m2 flat-plate collector with 1HP water pump and 325 gallons of water tank. A simulation model predicted the long-term thermal performance of the FPC.
The literature findings show that solar collector efficiency varies from 40 to 60% [18] as a function of inlet and ambient conditions as shown in Figure 5 [19]. The inputs for simulation include hot water usage pattern, system specifications and weather data. The time resolved weather data of interest is processed in “weather” block to feed into the thermal model represented by “collector”. A feedback ON-OFF control loop is in place between the collector outlet and demand side temperature (Ttank) shown by the “controller” block to trigger water through collector by sensing tank temperature and availability of resource (solar radiation).
 |
Fig. 4 Information flow diagram of TRNSYS for SWHS. |
2.2 Building typology
The building typology is defined by hot water use pattern and set point temperatures in the present study. In literature, several standard hot water usage patterns are reported for the US and Europe [20,21], while very little is available on the subject for hot weather as of UAE. The pattern shown in Figure 6 is used to estimate a standard demand for residential, hospital and office buildings [22–24] in the UAE. In the current simulations, the end use temperature is set at 45 °C for residential, school and office buildings and 65 °C for hospital buildings.
 |
Fig. 6 Hot water usage pattern for (a) residential (b) hospital (c) office [22–24] under the hot weather conditions as of UAE. |
3 Results and discussion
The thermal model developed in TRNSYS is validated with experimental data measured from a flat plate collector installed at the same site. Simulations are conducted employing typical means year (TMY-2) weather data for Abu Dhabi. The collector operational parameters of tilt angle, heat transfer fluid flow rate and heat loss coefficients are set in the TRNSYS model representing the experimental set up and ambient conditions. Temperatures were measured at front surface and leaving water from the collector and compared with the model prediction as shown in Figure 7. The results show a reasonable agreement between experimental and simulated temperatures with deviation of less than 5% at the most. The validated model is used to predict effects of collector operational parameters on the energy produced from the collector presented in the following sections.
 |
Fig. 7 The experimental and simulated temperatures of the absorber surface and water leaving the collector. |
3.1 Collector tilt angle
The performance of solar collector depends on its inclination angle [25,26]. Designers generally locate collectors on the building roof (pitched or flat) or on the façade (vertical wall). The same is simulated by varying monthly collector tilt angle (Φ) from 0° (representing flat roof) to 90° (representing south facing façade) with an increment of 5° representing various roof pitch angles while keeping at 0° azimuth representative of a south facing collector in the northern hemisphere. The average thermal gain (Qc) is plotted against Φ as shown in Figure 8 to determine the optimal Φ for each month. The Qc for January (winter) was 1.95 (kWh/m2) at Φ of 0° which kept increasing to reach at 3.25 (kWh/m2) at Φ of 50° (pitched roof). Beyond 50°, it kept dropping to reach to 2.2 (kWh/m2) at Φ of 90° (vertical wall). It can be deduced that 50° is the optimal pitch angle for south-facing collector in January for Abu Dhabi. Similarly, for summer months i.e. May, the average Qc was 4.11 (kWh/m2) at Φ of 0° which kept decreasing with increasing Φ to reach 0.75 (kWh/m2) at 90°, suggesting that 0° is the optimal Φ in May. Similarly, the optimal Φ for each month was determined based on maximal Qc presented in Table 2.
To determine the yearly optimal fixed pitch angle, the collector slope was varied from 12 to 36° to simulate the off-latitude collector performance by up to ±12°. The maximum yearly Qc of 1207.47 (kWh/m2) was obtained at 24°, the latitude of the place as shown in Figure 9, which agrees with previous findings [27]. The findings highlight that the collector performance can greatly be optimized by monthly adjustment of Φ instead of yearly fixed value with little to no additional cost while bringing substantial benefits.
The architects may encounter design-dictated situations to install collectors either as wall mounted (for high rise buildings) or roof installed (sloped or flat). Hence, knowing the compromise between the design preferences and the prospective energy production would be informative. Thus, the yearly thermal performance of the collector installed at a sloped roof of (24°), flat roof (0°) and vertical wall (90°) are compared in Figure 10. The results show that the collector installed on a sloped roof (latitude angle) performed the best, followed closely by the flat roof. The collector performance varied slightly with building type mainly due to effect of water flow rate.
 |
Fig. 8 Monthly average thermal energy (Qc) produced by solar collector at various tilt angles (Φ). |
Optimum monthly collector tilt angles for enhanced thermal energy gain.
 |
Fig. 9 Yearly thermal energy gain (Qc) of the collector at various tilt angles (Φ) to determine energy losses at the off optimal latitude scenarios. |
 |
Fig. 10 Thermal energy gain (Qc) of the collector installed at the pitched roof (24°), flat roof (0°) and vertical wall (90°). |
3.2 Azimuth angle
The optimal orientation is determined as south facing at zero azimuth (β). However, at times, designers are required to apply collectors deviating from south that may affect Qc [28]. The impact of varying β from 90° (east) to −90° (west) with an increment of 30° was, therefore, determined on Qc on a monthly and yearly basis as shown in Figure 11A and B. The results indicate that Qc peaked at β = 0° for all months. An interesting observation noted that in summer months (April to August) the collector performance remained unaffected by azimuth changes while during the rest of the year (September to March) the performance decreased sharply when moving away from the south orientation. Hence, yearly Qc of the south facing collector is 30% and 22% higher than that of west and east facing collector respectively.
 |
Fig. 11 (A) The impact of azimuth angle (β) on the average energy produced from the solar collector (Qc) on average monthly basis. (B) The impact of azimuth angle (β) on the energy produced from the solar collector (Qc) on yearly basis. |
3.3 Inlet flow rate
Daily water consumption for each building type is calculated per code requirements to size the collector tank and is kept fixed for the whole year. Since the collector only recovers thermal energy during the daytime, the varying daylight intensity and hours affect the amount of thermal energy available at the collector. The variable energy available at the absorber requires variable water flow rate for optimal energy recovery. The water flow rate inlet to the collector will in turn need to be optimized for different months. The total daily water demand is circulated through the collector during daytime (represented by daylight hours) at various flow rates to determine optimal flow rate for each month and building type. The summer months of May and June had the highest number of daylight hours with an average of 13 h, while the winter months of January and December had the lowest with an average of 10 h [29]. On the other hand, the heating demand naturally peaked in winter months compared to that of summer months. Additionally, each building type has different occupant loads and temperature set points which impact the optimal water flow rate for maximum thermal energy recovery. The inlet water flow rate for each of the building sector considered (residential, hospital, school, office, factories) is optimized for each month considering all the above-mentioned factors. Inlet water flow rate was found to be higher in winter months and lower in summer months yielding maximal thermal energy extraction as shown in Figure 12 while the hospital building required the highest and the most variable water flow rate.
 |
Fig. 12 Monthly average inlet water flow rate for different building type. |
3.4 Inlet water temperature
Since temperature of municipality supply water entering the collector is an uncontrolled parameter, its influences on the collector's performance is of interest specifically in UAE as it varies substantially among different seasons. The inlet water is assumed to be 3 to 4 °C higher than average daytime ambient temperature (Tavg-amb-day) considering the effect of ambient temperature and solar flux on the exposed storage tanks [30]. The Tavg-amb-day in UAE was the highest in May (42 °C) and the lowest in January (26 °C) [7]. Qc for each building type is plotted (left axis) with Tavg-amb-day (red line on right axis) as presented in Figure 13. At the lowest Tavg-water-inlet,Qc, is the highest and the vice versa which is in agreement with the collector efficiency curve shown in Figure 5. The results shown in Figure 13 confirm that the collector delivered higher thermal energy from September to April which coincides with the peak months of hot water demand. The occurrence of demand and supply peaks in the same season enabling the stakeholder to utilize maximum collector capacity.
 |
Fig. 13 Average energy contribution from the solar collector with varying inlet water temperature. |
3.5 Solar tracking
The regular building applied collectors for office, residential and commercial sectors were not tracked while tracking was considered for hospitals. However, the strong and stable radiation spanning over several daylight hours in UAE and similar contexts offers an opportunity to determine the potential enhancement in collector yield through solar tracking. The effect of solar tracking is investigated employing three tracking modes i.e., the surface rotates about a vertical axis (single-axis) to track the sun (track-1), the surface rotates about horizontal axis (single-axis) to track the latitude changes (track-2), the surface tracks in horizontal and vertical axis (double-axis) such that the beam radiation is always normal to the surface (track-3). The Qc of tracked collector is compared with that of a static collector facing south at optimal tilt angle (24°). The net Qc produced by collector in each tracking mode is calculated after subtracting the energy required for tracking of the collector and is presented in Figure 14. The net Qc for track-1, track-2, and track-3 was higher than that of static collector by 5.6%, 10.3% and 13.4% respectively indicating a potential to introduce tracking option. The simulation studies are pure energy comparisons and does not include the special and structural requirements of tracking systems which needs further analysis and is out of the scope of this paper.
 |
Fig. 14 Monthly average energy contribution from the solar collector with varying solar tracking modes. |
3.6 Solar concentration
The solar radiation as it reaches the collector surface (so called single sung) yields lower temperatures suitable for building applications that require water at 45 °C. However, for hospitals and industrial processes, the required temperatures range from 75 to 110 °C and is unlikely to be achieved by the conventional single sun collectors. To achieve such a higher temperature, modifications are required such as adding mirrors or lenses to concentrate solar radiation. The effect of solar concentration by employing geo-metrical concentration ratio (ratio of lenses or mirror area to the collector area) ranging from 1 to 5x are investigated in winter months (Dec. and Jan.) to determine their effectiveness in the worst-case scenario i.e., season of higher water demand with lower solar gains. An almost linear increase in collector outlet temperature was observed with increasing solar radiation concentration as shown in Figure 15. It was observed that without solar concentration (1x), the water temperature remained below 60 °C which can only serve domestic buildings with demand side temperature of 45 °C. The temperature required for hospital buildings (65 °C) is achieved with the concentration ratio of 2x and that required for industrial buildings (70 °C–110 °C) is achieved by concentration ratio of 3–5x. To achieve such temperatures, the collector needs modifications such as optical elements, tracking systems and structural support which involves additional space and cost which are not considered at this stage. The study therefore, is intended to determine achievable temperatures at certain concentration ratios only leaving the detailed resource input-output comparison for future studies.
 |
Fig. 15 Temperature variation versus solar radiation concentration. |
4 Overall system performance
Finally, the collector is simulated using optimal collector parameters of tilt angle, azimuth angle and water flow rate discussed in previous sections to determine its effectiveness in delivering the required amount of hot water [14] and at the desired temperature [15]. The thermal energy produced by the collector is compared to the thermal energy required by each building type for the required amount of hot water production. Finally, the ratio of collector area to building foot print area is calculated to deliver the required hot water demand for each building type as shown in Table 3. The results show that the hospital building required the highest collector area per building area associated to higher occupants’ density as well as hot water demand for specific activities such as equipment sterilization.
The calculated ratios should help building professionals and owners to size an optimal solar thermal collector for their respective buildings with minimal effort and yet be accurate. In design terms, however, opportunities may be sometimes limited, knowing that SWHS are traditionally installed on rooftops, the space availability may be limited due to building design (for example, in tall buildings) or the existence of other building equipment such as HVAC systems. The reported higher temperatures achieved by solar tracking and solar concentration can widen the integration of solar energy in novel areas like industries, nevertheless it comes at the expense of additional space by concentrators and tracking systems.
Energy performance of the optimized solar thermal collector for various building types under different tracking options.
5 Economic analysis of the system
The economic analysis is conducted by calculating simple payback period considering the benefit of energy produced and the cost of the systems installed. The energy is converted into monetary cost and benefit by applying UAE based electricity tariff of AED 0.32/kWh [31]. To apply the electrical energy tariffs, the thermal energy is converted into equivalent electrical energy by considering a 70% depreciation in energy quality. Additional tracking, inclusive of tracking system and energy, cost is counted as $0.36 per watt installed [32] considering thermal systems equivalent of PV systems in terms of tracking. Energy consumed by the pump to circulate water through collector is calculated by assuming 10 m additional water head with a flow rate of 0.18 L/. It resulted in the additional shaft power of 30 W for pumping. The equivalent electrical energy gain for static, single axis tracked (vertical), single axis tracked (horizontal), double axis tracked, and concentrated case is 35.3 MWh/lifetime, 37.5 MWh/lifetime, 39.2 MWh/lifetime, 40.6 MWh/lifetime and 50.6 MWh/lifetime respectively. The considered costs and benefits are compiled in Table 4.
The simple payback period is calculated by dividing the total cost of the system (initial investment as well as operating cost) by the economic benefit of the energy produced in the first year applying the values of energy harvested and electricity rates. The static case has the longest payback period of almost 3 years. Payback period reduced gradually with the improvement in thermal gain via different ways of tracking and/or concentration. In the optimized case, the payback period is reduced to almost 2 years.
Cost estimation of the set-ups and their monetary benefits.
6 Conclusion
This study examined the energy performance of SWHS in various building types under the hot climate of UAE, through TRNSYS simulation model. The parametric simulation determined the optimal collector parameters of tilt angle, azimuth angle and collector inlet water flow rate with respect to different seasons, building types and water demands. An optimal tilt angle of each month was identified to exploit the maximum potential of the system in Abu Dhabi, UAE which ranged from 50° at maximum for January to 0° for May. The optimum azimuth angle was found to be 0° (south facing) rendering a drop of 22% and 30% in thermal yield when the collector faced exact East and West respectively. It was observed that the roof applied collectors (both flat and pitched) are more effective than wall mounted collectors. Eventually, the collector area required per building area was determined for each building type with the hospital requiring, in the best case, the highest ratio value. The solar collector tracking was then evaluated as a means of reducing the area allocated to install the collectors on top of a roof or on a facade. The needs for solar radiation concentration is determined for some building types to deliver the higher required temperatures. It was also evident that the number of required collectors decrease for each building as the axis of tracking increases. Finally, the system feasibility is calculated for the payback period and the optimized case will be able to return its cost in almost 2 years.
These results would provide building professionals with a quick assessment of the possibility to integrate the required area or number of SWHS collectors to meet the hot water demand in new or retrofitted buildings.
Nomenclature
Ac: aperture area of the collector (m2)
CHX: heat-capacitance of coiled heat-exchanger (kJ/K)
Cpc: specific heat of collector fluid (kJ/(kg K))
Ctank: heat capacitance of storage tank (kJ/K)
fc: collector-fin efficiency factor
fr: overall collector heat-removal efficiency factor
Ib: incident-beam radiation per unit area (kWh/m2)
Id: diffused radiation per unit area (kWh/m2)
It: global radiation on horizontal surface per unit area (kWh/m2)
Iti: total incident-radiation on a flat surface per unit area (kWh/m2)
mc: collector fluid mass-flow rate (kg/h)
nc: number of collectors mounted in series
Qc: rate of heat gain collector array (kW)
Qin, HX: rate of heat gains of coiled heat-exchanger (kW)
Qin, tank: rate of heat gains of storage tank (kW)
Qout, HX: rate of heat loss of coiled heat-exchanger (kW)
Qout, tank: rate of heat loss from storage tank (kW)
SWHS: solar water heating systems
SHC: solar heating and cooling systems
Tav: collector-fluids average temperature (°C)
Thwa: hot-water average temperature (°C)
Thw1: hot-water initial temperature (°C)
Thw2: hot-water final temperature (°C)
THX: temperature of coiled heat-exchanger (°C)
Ti: temperature of fluid entering the collector (°C)
Tp: collector-plates temperature at stagnation (°C)
Ttank: temperature of storage tank (°C)
Ube: heat loss coefficient of collector bottom surface (kWh/ m2 K)
Uc: overall heat loss-coefficient of collector (kWh/ m2 K)
Symbols
α: absorptance of absorber plate
εg: emissivity of glass covers
εp: emissivity of absorber plate
σ: Stefan–Boltzmann constant (5.6697 × 10-8 W/ (m2 K4))
τ: transmittance of absorber plate
φ: collector latitude angle (°)
β: collector azimuth angle (°)
Acknowledgments
The authors gratefully acknowledge financial support from the United Arab Emirates University through the Emirates Centre for Energy and Environment research funded project (31R054).
References
- Dubai Electricity & Water Authority (DEWA), Annual Statistics, https://www.dewa.gov.ae/en/about-dewa/about-us/dewa-publications/annual-statistics [Google Scholar]
- U.S. Environmental protection agency, draft inventory of U.S. greenhouse gas emissions and sinks:1990–2014 (U.S. environmental protection agency, Washington, 2016) [Google Scholar]
- U.S. Energy information administration, issues in international energy consumption analysis: Canadian energy demand, (2015) [Google Scholar]
- R. Kempener, G. Simbolotti, G. Tosato, Solar Heating and Cooling for Residential Applications (International renewable energy agency, 2015) [Google Scholar]
- M.D. Islam, I. Kubo, M. Ohadi, A.A. Alili, Measurement of solar energy radiation in Abu Dhabi, UAE, Appl. Energy 86, 511–515 (2009) [CrossRef] [Google Scholar]
- A. Hasan, H. Alnoman, Y. Rashid, Impact of integrated photovoltaic-phase change material system on building energy efficiency in hot climate, Energy Build. 130, 495–505 (2016) [CrossRef] [Google Scholar]
- A. Hasan, K.A. Al-Sallal, H. Alnoman, Y. Rashid, S. Abdelbaqi, Effect of Phase Change Materials (PCMs) Integrated into a Concrete Block on Heat Gain Prevention in a Hot Climate, Sustainability 8, 1009 (2016) [CrossRef] [Google Scholar]
- F.A. Ghaith, R. Abusitta, Energy analyses of an integrated solar powered heating and cooling systems in UAE, Energy Build. 70, 117–126 (2014) [CrossRef] [Google Scholar]
- A. Al-Alili, M.D. Islam, I. Kubo, Y. Hwang, R. Radermacher, Modeling of a solar powered absorption cycle for Abu Dhabi, Appl. Energy 93, 160–167 (2012) [CrossRef] [Google Scholar]
- F. Jafarkazemi, S.A. Saadabadi, Optimum tilt angle and orientation of solar surfaces in Abu Dhabi, UAE, Renew. Energy 56, 44–49 (2013) [CrossRef] [Google Scholar]
- A. Khalil, A. Alnajjar, Experimental and theoretical investigation of global and diffuse solar radiation in the United Arab Emirates, Renew. Energy 6, 537–543 (1995) [CrossRef] [Google Scholar]
- A transient system simulation program-program manual, University of Wisconsin-Madison, USA: Solar energy laboratory, TRNSYS 17 (2004) [Google Scholar]
- International Building Code 2009, https://law.resource.org/pub/us/code/ibr/icc.ibc.2009.html [Google Scholar]
- ASHRAE HANDBOOK 2011 HVAC Applications SI Edition [Google Scholar]
- The engineering toolbox (2016), http://www.engineeringtoolbox.com/design-hot-water-system-d_92.html [Google Scholar]
- S.A. Klein, Calculation of flat-plate collector loss coefficients, Sol. Energy 17, 79–80 (1975) [Google Scholar]
- Solar-energy laboratory, IIsibat version 3.0.0.26, TRNSYS 15.3., Solar-energy laboratory university of Wisconsin Madison [Google Scholar]
- M.R. Islam, K. Sumathy, S.U. Khan, Solar water heating systems and their market trends, Renew. Sustain. Energy Rev. 17, 1–25 (2013) [CrossRef] [Google Scholar]
- I.R. Pillai, R. Banerjee, Impact of hot water usage pattern and location on economics of solar water heating systems, Water Energy Abstr. 14, (2004) [Google Scholar]
- A. Lowenstein, C. C. Hiller, Disaggregating residential hot water use − Part II', ASHRAE Trans. 104, 1852–1863 (1998) [Google Scholar]
- NAHB Research Center, Inc (2002), Performance comparison of residential hot water systems, Report prepared for National Renewable Energy Laboratory, Colorado [Google Scholar]
- A. Gadgil, Economic, materials and performance constraints on the design of a solar DHW system for use in India, SESI J. 1, 31–36 (1987) [Google Scholar]
- I.R. Pillai, R. Banerjee, Methodology for estimation of potential for solar water heating in a target area, Sol. Energy 81, 162–172 (2007) [CrossRef] [Google Scholar]
- K. L. Narkhede, Solar water heater as a demand side management option, M. Tech. Dissertation, Energy Systems Engineering, (Indian Institute of Technology, Bombay, India, 2001) [Google Scholar]
- A. Shariah, M.A. Al-Akhras, I.A. Al-Omari, Optimizing the tilt angle of solar collectors, Renew. Energy 26, 587–598 (2002) [CrossRef] [Google Scholar]
- H. Moghadam, F.F. Tabrizi, A.Z. Sharak, Optimization of solar flat collector inclination, Desalination 265, 107–111 (2011) [CrossRef] [Google Scholar]
- M.D. Islam, A.A. Alili, I. Kubo, M. Ohadi, Measurement of solar-energy (direct beam radiation) in Abu Dhabi, UAE, Renew. Energy 35, 515–519 (2010) [CrossRef] [Google Scholar]
- M. Kacira, M. Simsek, Y. Babur, S. Demirkol, Determining optimum tilt angles and orientations of photovoltaic panels in Sanliurfa, Turkey, Renew. Energy 29, 1265–1275 (2004) [CrossRef] [Google Scholar]
- L. El Chaar, L.A. Lamont, Global solar radiation: multiple on-site assessments in Abu Dhabi, UAE, Renew. Energy 35, 1596–1601 (2010) [CrossRef] [Google Scholar]
- A. Hasan, H. Alnoman, A.H. Shah, Energy efficiency enhancement of photovoltaics by phase change materials through thermal energy recovery, Energies 9, 782 (2016) [CrossRef] [Google Scholar]
- Dubai Electricity & Water Authority − tariff, https://www.dewa.gov.ae/en/customer/services/consumption-services/tariff [Google Scholar]
- Solar Balance-of-System: To Track or Not to Track, Part I, https://www.greentechmedia.com/articles/read/solar-balance-of-system-to-track-or-not-to-track-part-i [Google Scholar]
Cite this article as: K.T. Aoul, A. Hasan and H. Riaz: Solar water heating systems for different buildings under a hot climate; parametric optimization and economic analysis. Sust. Build. 3, 3 (2018).
All Tables
Hot water demand and water temperature per building type of a set area of 1000 m2.
Energy performance of the optimized solar thermal collector for various building types under different tracking options.
All Figures
 |
Fig. 1 Growth of electricity consumption and generation in Dubai, United Arab Emirates (UAE) [1]. |
| In the text | |
 |
Fig. 2 Electricity consumption in different sectors of Dubai, United Arab Emirates (UAE) [1]. |
| In the text | |
 |
Fig. 3 Information flow diagram of micro-simulation for SWHS [19]. |
| In the text | |
 |
Fig. 4 Information flow diagram of TRNSYS for SWHS. |
| In the text | |
 |
Fig. 5 Solar collector efficiency curve [19]. |
| In the text | |
 |
Fig. 6 Hot water usage pattern for (a) residential (b) hospital (c) office [22–24] under the hot weather conditions as of UAE. |
| In the text | |
 |
Fig. 7 The experimental and simulated temperatures of the absorber surface and water leaving the collector. |
| In the text | |
 |
Fig. 8 Monthly average thermal energy (Qc) produced by solar collector at various tilt angles (Φ). |
| In the text | |
 |
Fig. 9 Yearly thermal energy gain (Qc) of the collector at various tilt angles (Φ) to determine energy losses at the off optimal latitude scenarios. |
| In the text | |
 |
Fig. 10 Thermal energy gain (Qc) of the collector installed at the pitched roof (24°), flat roof (0°) and vertical wall (90°). |
| In the text | |
 |
Fig. 11 (A) The impact of azimuth angle (β) on the average energy produced from the solar collector (Qc) on average monthly basis. (B) The impact of azimuth angle (β) on the energy produced from the solar collector (Qc) on yearly basis. |
| In the text | |
 |
Fig. 12 Monthly average inlet water flow rate for different building type. |
| In the text | |
 |
Fig. 13 Average energy contribution from the solar collector with varying inlet water temperature. |
| In the text | |
 |
Fig. 14 Monthly average energy contribution from the solar collector with varying solar tracking modes. |
| In the text | |
 |
Fig. 15 Temperature variation versus solar radiation concentration. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


