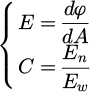| Issue |
Sust. Build.
Volume 7, 2024
|
|
|---|---|---|
| Article Number | 3 | |
| Number of page(s) | 7 | |
| Section | Advanced Daylight Systems and Lighting Performance | |
| DOI | https://doi.org/10.1051/sbuild/2024003 | |
| Published online | 19 June 2024 | |
Original Article
Research on daylighting optimization of building space layout based on parametric design
School of Design, Henan Mechanical and Electrical Vocational College, Zhengzhou, Henan 450000, PR China
* e-mail: llil85@outlook.com
Received:
15
March
2024
Accepted:
17
May
2024
Excellent daylighting in buildings is beneficial to protect the physical and mental health of users. After introducing the daylighting of the building, this paper used the genetic algorithm (GA) optimized by co-evolution to optimize the daylighting. Then, a one-story L-shaped accommodation house in Zhengzhou, Henan Province was taken as a case for analysis. The effectiveness of the Daysim software used for calculating the building lighting indicator was tested. Then, the performance of the improved GA with different daylighting indicators as fitness values was compared. Finally, the optimization performance of the particle swarm optimization (PSO) algorithm, the traditional GA, and the improved GA were compared. The results showed that the daylighting indicators simulated by Daysim were significantly correlated with the measured data, suggesting its effectiveness. The improved GA using dynamic daylighting indicators as fitness values had better optimization performance. Compared with the other two algortihms, the improved GA had better optimization performance.
Key words: Parameterization / architectural design / daylighting / genetic algorithm
© L. Li, Published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Except for some buildings for special purposes, most buildings will consider daylighting in the design process, and with the improvement of construction technology and people’s living standards, the demand for building daylighting also increases [1]. Experienced designers are often responsible for traditional architectural design and will ensure the daylighting of buildings according to their own experience [2]. However, the daylighting designed by experience can only be regarded as just right rather than optimal in most cases, and it still needs to be adjusted according to the actual situation after it is put into use, but the building structure can not be greatly changed at this time [3]. Through the computer parametric design, designers can replicate the illumination conditions within buildings and adjust the structural parameters to better control the daylighting of buildings. Futrell et al. [4] proposed a method to enhance the daylighting efficiency of intricate architectural structures. They used dynamic climate-based lighting simulation. The simulation results verified the effectiveness of the algorithm. Dino et al. [5] created a tool for optimizing designs, known as multi-objective architectural design explorer (MADE), and used a design exploration strategy to facilitate Pareto-based comparative search. Yao et al. [6] simulated the daylight distribution of a typical small residential room that had obstructions positioned in front of its windows. The results showed that the indoor daylighting could be improved through the optimization of the interior facade. Zhang et al. [7] used Rhino3D and Grasshopper plugins to construct an architectural model and employed the Octopus plugin in Grasshopper for iterative calculation of target values, addressing multi-objective balance issues. The results showed that the optimized office layout achieved energy-saving optimization in terms of energy consumption, daylighting, and thermal comfort. Wang et al. [8] first obtained residents’ spatial requirements through questionnaires and then utilized the Grasshopper platform to establish a baseline model. They subsequently employed building simulation plugin Ladybug Tools and multi-objective optimization tool Wallacei to optimize bedroom location, orientation, bay window size, depth to bay ratio, window form, window-to-wall ratio, and horizontal shading width based on daylight autonomy (DA), useful daylight illuminance (UDI), and proportion of discomfort hours (PDH) as indicators for daylighting and thermal comfort. The study conducted by Fang et al. [9] utilized redirecting complex fenestration system for indoor daylighting improvement and compared the annual daylight performance and glare levels of three complex fenestration systems with dynamic metal louvers, micro-louver film, and dynamic micro-prism film louvers using the five-phase method. The results showed that the combined dynamic louvers reduced the discomfort glare occurrence rate by 68.9%. In the above-mentioned literature, research has been conducted on optimizing the daylighting performance of buildings. The steps involve establishing a building model and then setting environmental conditions to calculate the daylighting performance of the building. The difference lies in the platform used for constructing the building model and the methods employed to optimize building parameters. In this study, a conventional approach was followed to construct the building model, and a genetic algorithm (GA) was used for optimizing its parameters. Building lighting simulation software was utilized to calculate dynamic daylighting indicators as guidance for the algorithm, while co-evolution was also employed to enhance the performance of the GA. This paper briefly introduces the lighting performance of buildings, as well as the static and dynamic lighting indicators. The GA was employed to optimize the lighting performance of buildings. Moreover, co-evolution was introduced into the GA to enhance the optimization performance of the algorithm. Then, a one-story L-shaped accommodation house in Zhengzhou, Henan Province was taken as a case for analysis. The innovation of this article lies in using building lighting environment simulation software to calculate the dynamic daylighting indicators of buildings, in order to guide the optimization direction of the GA and make the optimization results more realistic. Additionally, co-evolution was introduced to enhance the performance of the GA. The limitation of this article is that building parameter optimization mainly focuses on easily adjustable parameters such as wall-to-window ratio, window transmittance, and sky obstruction angle. In other words, the optimization in this article primarily focuses on fine-tuning existing buildings. Therefore, future research should focus on overall planning for new buildings.
2 Methods and materials
2.1 Case overview
In this paper, a one-story L-type accommodation house in Zhengzhou City, Henan Province was taken as a case to analyze. Figure 1 is the planar sketch of the analyzed object. There are five rooms of the same size in this room, and each room has a door and two windows. The measured fundamental parameters of the single room are shown in Table 1. As the L-shaped accommodation room has been built, its overall structure cannot be adjusted. The parts that can be adjusted are the wall-to-window ratio of the room [10], the window transmittance, and the sky occlusion angle. Therefore, when the improved GA was used to optimize the room, the wall-to-window ratio, window transmittance, and sky occlusion angle were used for coding [11]. The wall-to-window ratio was adjusted from 0.3 to 0.7. The window transmittance was adjusted from 0.2 to 0.7. The sky occlusion angle was adjusted from 0° to 90°.
Zhengzhou is located in the central region of China, which belongs to the warm temperate subhumid climate zone [12], with the characteristics of four distinctive seasons and large temperature differences. In terms of temperature, the average annual temperature in Zhengzhou is 14.2 °C. The highest temperature usually appears in summer, generally around 30 °C, and the lowest temperature is usually in winter, generally falling below 0 °C.
 |
Fig. 1 Schematic diagram of a one-story L-shaped accommodation house in Zhengzhou. |
Basic parameters of a single room within the L-shaped accommodation house.
2.2 The optimization algorithm
In this paper, parametric design is used to optimize the daylighting properties of buildings, and the steps can be roughly divided into two steps. The first step is to construct a mathematical model of building daylighting performance indicators related to building parameters. The equation of the model is:
where E is the illuminance of a point on the light plane [13], dφ is the luminous flux of the point, dA is the unit area of the point, C is the daylighting coefficient of a point on the light plane, En is the illuminance of the point, and Ew is the outdoor diffuse illuminance measured at the same time. Daylighting uniformity is the ratio between the minimum value of E or C and the average. The closer the ratio is to 1, the more uniform the daylighting will be. However, the static daylighting indicators are calculated using the all-overcast sky model [14], which is not exactly the same as the actual lighting environment faced by buildings. Building light environment simulation software can simulate not only the fixed lighting environment but also the dynamic changes of natural lighting, especially after importing weather data. Therefore, dynamic daylighting indicators are used to measure the daylighting performance of buildings, including DA and UDI. DA refers to the proportion of time in the year when the illuminance of the plane measurement points in a building is higher than the minimum standard under the natural light environment. UDI refers to the proportion of time in the whole year when the illuminance of the plane measurement points in a building is within the effective range under the natural light environment [15].
The second step is to solve the daylighting model of the building using an optimization algorithm. In this paper, we choose a genetic algorithm improved by cooperative coevolution for optimization. The process is as follows.
The building parameters are input, and a building model is constructed according to the parameters [16].
Three initial populations are generated according to the parameters needed to be optimized in the building. In the three populations, the number of particles is the same, but the genes of chromosomes are different. Moreover, it is necessary to pay attention to the adjustment range of corresponding parameters when randomly generating chromosome genes.
The chromosomes in the population are decoded to obtain the building optimization parameters corresponding to each chromosome, and then the optimized parameters are substituted into the building model. Each chromosome corresponds to an adjusted building model.
The daylighting performance of the adjusted model is calculated. Daysim simulation software [17] is employed to calculate the daylighting performance indicator of buildings. Daysim can simulate the distribution of daylight and the lighting in buildings at different times and under different weather conditions. At the same time, the software itself also has the function of creating 3D building models. It can set different windows, doors, curtains, and other openings and adjust the material properties and light source parameters. This software combines the construction of the building model and the calculation of daylighting performance indicators into one, which greatly facilitates the optimization of building daylighting [18].
Whether the algorithm ends the optimization is determined. If it ends, the optimization scheme of building parameters corresponding to the optimal chromosome in the population will be output. If it is not finished, it enters the next step.
Collaborative genetic operations are carried out on the three populations, and the best particles of the population are used to replace the worst particles in other populations. After that, the optimal part of the chromosomes in the respective populations are directly selected as the offspring chromosomes, and the remaining chromosomes are operated by “crossover” and “mutation”. Crossover operation is an operation in which any two chromosomes exchange genes on the same gene segment according to the crossover probability. Mutation operation refers to any chromosome randomly changing on a gene segment according to the mutation probability (not exceeding the parameter range corresponding to the segment).
2.3 Parameter settings
Table 2 shows the relevant parameters of the improved GA.
In addition, this paper also tested two other optimization algorithms for comparison. They were the traditional GA and the particle swarm optimization (PSO) algorithm. The related parameters of the traditional GA are as follows. Thirty chromosomes were randomly generated in a population according to the limited range. The top six chromosomes were selected as the offspring. The crossover and mutation were the same as the improved GA, and the number of iterations was also 100.
The relevant parameters of the PSO algorithm are as follows. Thirty particles were randomly generated by the population according to the restrictions, the two learning factors were 1.5, the inertia weight was 0.8, and the maximum number of iterations was 100.
Parameters of the improved GA.
2.4 Validation of model daylighting simulation
Daysim software has been introduced in the previous text, which can not only model the building but also simulate the building’s light environment. Because this paper uses Daysim simulation to calculate the daylighting indicators as the fitness value of the optimization algorithm, and the accuracy of these indicators will directly affect the accuracy of the optimization algorithm, so to ensure the accuracy of the optimization algorithm, first of all, the validity of Daysim simulation calculation of daylighting index was verified. The correlation analysis was carried out between the simulated illuminance and the locally measured data in the accommodation room.
Firstly, the actual illumination was measured. The required tools included an illuminometer (Japan Sekonic, C-7000 model), a range finder (SNDWY, SW-M50 model), and a steel tape measure. The steps for the actual measurement of the illuminance of the accommodation room are shown below.
Selection of the test time: According to the local climatic conditions of Zhengzhou, a day with stable sunshine was selected under cloudy weather from February to April to conduct the illuminance measurement of the accommodation room. The measurement period of a day was from 8 am to 10 am and from 2 pm to 4 pm, and the illuminance was measured at the measurement point every hour.
Setting of measuring points: The measurement points were set at the center point and four corners of each room 1 m above the ground, and there were a total of 25 measurement points. The weather on that day is partly cloudy with a temperature range of 15 °C to 22 °C, accompanied by a southeast wind.
Illuminance test: When conducting the illuminance test, the measuring personnel wore black clothing to avoid interference with the illuminance meter. At the set time point, the light receiver of the illuminance meter was placed horizontally at the measurement point and away from the illuminance meter. Each measuring point was measured three times, and the final average was taken.
After obtaining the measured illuminance value, the relevant parameters of the L-shaped accommodation room were input into Daysim for building modeling. After inputting the local weather data (from the Central Meteorological Network nmc.gov.cn/index.html), the daylighting performance was calculated to obtain the simulated value. A Pearson correlation analysis was used to analyze the measured and simulated illuminance values.
3 Results
To ensure the accuracy of the optimization algorithm, the validity of the daylighting performance calculated by the simulation software was verified. The correlation analysis was carried out between the measured illuminance of the accommodation room and the calculated illuminance of the simulation software, and the validity of the calculated values of the simulation software was verified according to the significance of the correlation. The correlation analysis results are shown in Table 3. It can be seen that the correlation coefficient between the measured and simulated illuminance was 0.968, and its Sig. was 0.001, indicating that the correlation was significant. Therefore, the improved GA and the other two optimization algorithms used for comparison could use the Daysim simulation software to calculate the daylighting performance indicators to optimize the building parameters.
In the process of optimization of the improved GA, the fitness value as the guidance of the optimization direction could be both the static daylighting indicators and the dynamic daylighting indicators. Therefore, the improved GA using different daylighting indicators as the fitness value was compared, as shown in Table 4. It can be seen that whether the static daylighting indicators or the dynamic daylighting indicators were used as the fitness value, the building parameter schemes optimized by the two algorithms could effectively improve the DA and UDI of the building compared with the initial scheme. In addition, the optimization scheme using the dynamic daylighting indicators as the fitness value had a better improvement effect, so the dynamic daylighting indicators were used as the fitness values in the subsequent comparison with the other two optimization algorithms.
To test the optimization performance of the improved GA, it was compared with the other two optimization algorithms, and the optimization schemes obtained by the three algorithms are shown in Table 5. It can be seen that compared with the initial scheme, the DA and UDI of the building parameters optimized by the three optimization algorithms were improved, but the improvement amplitude was not the same. The building parameter scheme optimized by the improved GA had the highest DA and UDI, the traditional GA was second, and the PSO algorithm was the lowest. The improved GA required the least number of iterations for the fitness value to converge to stability and consumed the least amount of time to compute optimized results.
Correlation analysis results of measured and simulated illuminance.
Optimization results of the improved GA with different daylighting indicators as fitness values.
Optimization schemes of three optimization algorithms for building daylighting performance.
4 Discussion
In addition to buildings with specific purposes, most buildings ensure sufficient daylighting during the design process, and there is also a certain level of expertise in designing for daylighting. Insufficient or excessive daylighting can both affect the user experience of a building, so it is necessary to set reasonable parameters related to daylighting in the design. Traditionally, experienced designers make adjustments based on their expertise, but the parameters set using this method are often generic solutions that provide just enough daylight rather than optimal lighting conditions. With the development of computer technology, architectural design schemes can be parameterized and digital models of buildings can be constructed within computers. Adjustments to the parameters of a building can be intuitively reflected in the digital model, including its daylighting performance. In this paper, after constructing a mathematical model for building daylighting performance, a GA was used to optimize the parameters of the mathematical model and employed co-evolutionary techniques to enhance the optimization capability of the GA. Subsequently, a case study was conducted on an L-shaped residential building in Zhengzhou City, Henan Province. The results obtained were as described above. Firstly, the effectiveness of Daysim simulation software for simulating building daylighting was validated. Then, it was confirmed that using dynamic daylighting indicators could lead to better optimization solutions. Finally, the results demonstrated that the GA improved by co-evolutionary techniques could achieve superior parameter solutions. The reason for this is that the static daylighting index calculates the lighting performance of buildings using a sky model for overcast conditions, assuming that the building is constantly in an environment with cloudy skies. However, this scenario clearly does not reflect reality. On the other hand, dynamic daylighting index simulates natural lighting by importing weather data into lighting simulation software, which provides a more realistic representation of lighting conditions compared to static daylighting index. Consequently, it yields more accurate results regarding daylighting performance. The GA treats the building parameters to be optimized as genetic fragments in chromosomes and adjusts these parameters through genetic operations guided by the fitness function (dynamic daylighting index), ultimately obtaining optimal building parameters. Compared to the PSO algorithm, the mutation operation in the GA is more likely to help chromosomes escape from local optima and continue evolving towards the global optimum. Furthermore, with the introduction of coevolutionary concepts, the GA synchronizes the evolution of three populations, expanding the search space. The chromosome exchange between these populations introduces new variations, further avoiding local optima and ultimately obtaining the best architectural parameter optimization solution.
5 Conclusion
This paper briefly introduces the lighting performance of buildings, as well as the static and dynamic lighting indicators, and to used the GA to optimize the lighting performance of buildings. At the same time, co-evolution was introduced into the GA to improve the optimization performance of the algorithm. Firstly, the effectiveness of Daysim software used to calculate building daylighting indicators was tested, and then the performance of the improved GA with different daylighting indicators as fitness values was compared. Finally, the optimization performance of the PSO algorithm, traditional GA, and improved GA was compared. There was a significant correlation between the measured and simulated illuminance of the accommodation room, suggesting that the daylighting performance indicators calculated by the Daysim simulation could be used to optimize the GA. Both static and dynamic daylighting indicators could be used to optimize the GA, but using dynamic daylighting indicators as fitness values achieved a better optimization scheme. The building parameter scheme optimized by the improved GA had the highest DA and UDI, the traditional algorithm was the second, and the PSO algorithm was the lowest. The improved GA required the least number of iterations for the fitness value to converge to stability and consumed the least amount of time to compute optimized results.
Funding
This article received no external funding.
Conflicts of interest
The author declares no conflict of interests.
Data availability statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Author contribution statement
Li Li designed research, performed research, analyzed data, and wrote the paper.
References
- F. Salata, I. Golasi, M. di Salvatore, A.L. Vollaro, Energy and reliability optimization of a system that combines daylighting and artificial sources. A case study carried out in academic buildings, Appl. Energ. 169, 250–266 (2016) [Google Scholar]
- A. Hammad, A. Akbarnezhad, H. Grzybowska, P. Wu, X. Wang, Mathematical optimisation of location and design of windows by considering energy performance, lighting and privacy of buildings, Smart Sustain. Built 8, 117–137 (2019) [CrossRef] [Google Scholar]
- Q. Gao, Y. Yang, Q. Wang, An integrated simulation method for PVSS parametric design using multi-objective optimization, Front. Architect. Res. 11, 509–526 (2022) [CrossRef] [Google Scholar]
- B.J. Futrell, E.C. Ozelkan, D. Brentrup, Optimizing complex building design for annual daylighting performance and evaluation of optimization algorithms, Energ. Buildings 92, 234–245 (2015) [CrossRef] [Google Scholar]
- I.G. Dino, G. Ucoluk, Multiobjective design optimization of building space layout, energy, and daylighting performance, J. Comput. Civil Eng. 31, 4017025.1–4017025.18 (2017) [Google Scholar]
- Y. Lu, T. Wolf, J. Kang, Optimization of facade design based on the impact of interior obstructions to daylighting, Archit. Simul. 009, 1–14 (2016) [Google Scholar]
- J. Zhang, L. Ji, S. Cunha, Optimization and prediction of energy consumption, daylighting, and thermal comfort of buildings in tropical areas, Adv. Civ. Eng. 2022, 1.1–1.14 (2022) [Google Scholar]
- J. Wang, J. Guo, Multiobjective optimization of the intergenerational residential space with the goal of daylighting and thermal comfort, J. Green Build. 18, 225–244 (2023) [CrossRef] [Google Scholar]
- J. Fang, Y. Zhao, Z. Tian, P. Lin, Analysis of dynamic louver control with prism redirecting fenestrations for office daylighting optimization, Energ. Buildings 262, 1–21 (2022) [Google Scholar]
- M. Talaei, M. Mahdavinejad, R. Azari, A. Prieto, H. Sangin, Multi-objective optimization of building-integrated microalgae photobioreactors for energy and daylighting performance, J. Build. Eng. 42, 102832 (2021) [CrossRef] [Google Scholar]
- Y. Dong, C. Sun, Y. Han, Q. Liu, Intelligent optimization: a novel framework to automatize multi-objective optimization of building daylighting and energy performances, J. Build. Eng. 43, 102804 (2021) [CrossRef] [Google Scholar]
- Y. Fang, S. Cho, Design optimization of building geometry and fenestration for daylighting and energy performance, Sol. Energy 191, 7–18 (2019) [CrossRef] [Google Scholar]
- L. Zhu, B. Wang, Y. Sun, Multi-objective optimization for energy consumption, daylighting and thermal comfort performance of rural tourism buildings in north China, Build. Environ. 176, 106841 (2020) [CrossRef] [Google Scholar]
- H. Aria, H. Akbari, Optimisation of night-time ventilation parameters to reduce building”s energy consumption by integrating DOE2 and MATLAB, Int. J. Sol. Energy 34, 516–527 (2015) [Google Scholar]
- C. Mihail-Bogdan, I. Constantin, N. Horia, The influence of genetic algorithm parameters over the efficiency of the energy consumption estimation in a low-energy building &z.star;, Energy Proc. 85, 99–108 (2016) [CrossRef] [Google Scholar]
- X. Wang, W. Cai, J. Lu, Y. Sun, L. Zhao, Model-based optimization strategy of chiller driven liquid desiccant dehumidifier with genetic algorithm, Energy 82, 939–948 (2015) [CrossRef] [Google Scholar]
- M. Kaliappan, S. Augustine, B. Paramasivan, Enhancing energy efficiency and load balancing in mobile ad hoc network using dynamic genetic algorithms, J. Netw. Comput. Appl. 73, 35–43 (2016) [CrossRef] [Google Scholar]
- Q. Deng, X. Gao, H. Zhou, W. Hu, System modeling and optimization of microgrid using genetic algorithm, Energy Energy Conserv. 1, 540–544 (2015) [Google Scholar]
Cite this article as: L. Li: Research on daylighting optimization of building space layout based on parametric design. Sust. Build. 7, 3 (2024).
All Tables
Optimization results of the improved GA with different daylighting indicators as fitness values.
Optimization schemes of three optimization algorithms for building daylighting performance.
All Figures
 |
Fig. 1 Schematic diagram of a one-story L-shaped accommodation house in Zhengzhou. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.